Otra demostración del teorema de Beatty
Pedro González Ruiz
Introducción y ejemplos
En éste artículo se da una demostración del teorema de Beatty. Para entenderlo bien, vamos a mostrar varios ejemplos, pero antes de eso recordamos una función muy importante en matemáticas, la parte entera o suelo de x, escrita como ⌊x⌋, que se define como el entero más cercano a x por defecto. Por ejemplo:
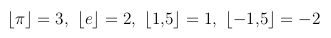
Veamos ahora varios ejemplos de lo que queremos mostrar:
-
En primer lugar elegimos el conocido número π ≅ 3.141592..., y a partir de él consideramos la sucesión
N(π) = {⌊π⌋, ⌊2π⌋, ⌊3π⌋, ...}
La notación N(π) sugiere los números naturales generados por π. Los 10 primeros términos de esta sucesión son
{3, 6, 9, 12, 15, 18, 21, 25, 28, 31}
Seguimos con el conjugado de π, en concreto τ = π/(π - 1) ≅ 1.466942 (1/π + 1/τ = 1). Al igual que antes consideramos la sucesión
N(τ) = {⌊τ⌋, ⌊2τ⌋, ⌊3τ⌋, ...}
Los 10 primeros términos de esta sucesión son
{1, 2, 4, 5, 7, 8, 10, 11, 13, 14}
Una simple observación nos muestra que no hay números comunes entre las sucesiones primera y segunda, y parece que todos los números naturales {1, 2, 3, 4, 5,...} se reparten entre ambos, es decir, el 1 y 2 están en la segunda, el 3 en la primera, el 4 y 5 en la segunda, el 6 en la primera, el 7 y 8 en la segunda, etc., y claro, la pregunta que nos viene enseguida es si esto es una particularidad del número π y su conjugado τ = π/(π - 1), o es general.
-
En segundo lugar consideremos el número √2 ≅ 1.41421..., y como antes la sucesión
N(√2) = {⌊√2⌋, ⌊2√2⌋, ⌊3√2⌋, ...}
Los 10 primeros términos son
{1, 2, 4, 5, 7, 8, 9, 11, 12, 14}
El conjugado de √2, es τ = √2/(√2 - 1) = 2 + √2 (1/√2 + 1/τ = 1). Al igual que antes
N(τ) = {⌊2+√2⌋, ⌊2(2+√2)⌋, ⌊3(2+√2)⌋, ...}
cuyos 10 primeros términos son
{3, 6, 10, 13, 17, 20, 23, 27, 30, 34}
Observamos lo mismo, es decir, en apariencia no hay números comunes entre las sucesiones primera y segunda, y parece que todos los números naturales se reparten entre ambos, es decir, el 1 y 2 caen en el primero, el 3 en el segundo, el 4 y 5 en el primero, el 6 en el segundo, el 7 y 8 en el primero, etc.
-
Veamos un tercer y último ejemplo. Sea ahora f = 5/3 ≅ 1.666666... y la sucesión
N(f) = {⌊f⌋, ⌊2f⌋, ⌊3f⌋, ...}
Los 10 primeros términos son
{1, 3, 5, 6, 8, 10, 11, 13, 15, 16}
El conjugado de f, es τ = f/(f - 1) = 5/2 (1/f + 1/τ = 1). Al igual que antes
N(τ) = {⌊τ⌋, ⌊2τ⌋, ⌊3τ⌋, ...}
cuyos 10 primeros términos son
{2, 5, 7, 10, 12, 15, 17, 20, 22, 25}
Observamos que ahora no es lo mismo que antes pues aparecen números comunes en ambos conjuntos, en concreto, 5, 10 y 15 están en ambos, y la segunda condición tampoco se cumple, ya que los números 4, 9, 14, por ejemplo, no aparecen por ningún lado.
En fin, la pregunta es elemental, en concreto, ¿qué condiciones deben cumplirse para que todos los números naturales se repartan entre los dos conjuntos de forma que no haya repeticiones?. La respuesta es que el número elegido debe ser irracional, es decir, que no sea un cociente de dos enteros y además, mayor que 1. La demostración de esta afirmación es el teorema de Beatty, el cual afirma que si ξ es cualquier número irracional, ξ > 1, y τ = ξ / (ξ - 1) es su conjugado, entonces, los dos conjuntos N(ξ) = {⌊ξ⌋, ⌊2ξ⌋, ⌊3ξ⌋, ...} y N(τ) = {⌊τ⌋, ⌊2τ⌋, ⌊3τ⌋, ...} contienen a todos los números naturales y solo una vez.
El artículo que sigue comienza con una introducción a las funciones suelo, techo y mantisa, demostrando las propiedades elementales de estas funciones. Acto seguido se discute y resuelve una ecuación diofántica y finalmente, se da una demostración del teorema de Beatty.