Colas y colas circulares en C
Pedro González Ruiz
Colas
Una cola es una estructura de datos tipo FIFO (First In, First Out), es decir, el primero que entra es el primero que sale, lo que significa que el primer elemento que llegue a la cola es el primero que debe ser tratado. Su nombre viene de la analogía con una ventanilla de atención a personas, en que el primero que llega es el primero en ser atendido, y todos aquellos que van llegando, se van situando a continuación uno del otro a la espera de que les llegue el turno.
En todo lo que sigue, cada elemento de la cola será una estructura, en el sentido del lenguaje C, y una cola será un vector de estructuras. Si m es el número de elementos de este vector, es decir, el número de estructuras, la cola no puede almacenar más de m elementos, y los datos serán numerados por índices que varían entre 0 y m-1.
Las colas son un ejemplo de estructura dinámica, ya que el número de elementos varía, y a la vez, estática, pues no puede crecer más de m.
Colas corriendo datos
Siguiendo el convenio anterior, la imagen mental de una cola es la que expresa la siguiente figura:
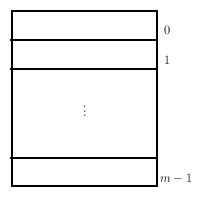
Todos los elementos se recuperan por el frente, en este caso, el elemento de índice 0. Sea pos un entero, el cual define el índice del primer lugar libre. La cola está vacía cuando pos = 0 y llena cuando pos = m, ya que hay solamente m lugares para almacenar. El aspecto es el siguiente (las zonas sombreadas indican lugares ocupados):

Veamos ahora las operaciones a realizar:
Insertar un elemento en la cola
El algoritmo es:

Extraer un elemento de la cola
El algoritmo es:

La notación di+1 -> di significa que el elemento situado en la posición i+1 debe ser copiado a la posición i. Esto es lo que ocurre en la vida cotidiana, en concreto, cuando una persona ha acabado su gestión en la ventanilla y la abandona, los demás deben moverse hacia adelante, es decir, el segundo pasa a ser el primero, el tercero al segundo y así sucesivamente. Para una cola pequeña, este algoritmo es sencillo y eficaz, pero cuando la cola es grande, el corrimiento de datos puede suponer un gasto de tiempo que enlentece el programa, razón por la cual, mostramos a continuación otro procedimiento mucho mejor para evitar este problema.
Colas circulares
Introducción al operador módulo
Antes de entrar en detalles, recordemos el operador módulo, que en el lenguaje C, se representa por %. Sea m un entero mayor que cero. La expresión a % m representa el resto de la división entre a y m. Por las propiedades de la división, si r = a % m, entonces, el entero r es tal que 0 ≤ r < m. Cuando r = 0, la división es exacta. Por ejemplo, 27 % 6 = 3, ya que al dividir 27 entre entre 6 resulta un resto de 3. Análogamente, 27% 9 = 0, pues al dividir 27 entre entre 9 resulta un resto de 0.
Operando módulo m solamente pueden aparecer los números:
0, 1, 2, ..., m-1
Si contamos de 1 a 10 módulo 7, los restos son:1 % 7 = 1, 2 % 7 = 2, 3 % 7 = 3, 4 % 7 = 4, 5 % 7 = 5, 6 % 7 = 6, 7 % 7 = 0, 8 % 7 = 1, 9 % 7 = 2, 10 % 7 = 3
La situación es idéntica a la que se presenta en el cuentakilómetros de un coche, una vez llegado al límite, el contador vuelve a 0.
Concepto de cola circular
El ambiente es el mismo que en la sección anterior, en concreto, disponemos de un vector de estructuras donde almacenar los datos. Sea m el número de estructuras. La cola no puede almacenar más de m elementos y los datos los numeramos como siempre, por índices que varían entre 0 y m-1 (ver figura siguiente):

Hacemos la estructura circular, identificando el siguiente de m-1 con 0, en otras palabras, operamos módulo m. Sea n el número de elementos de la cola (0 ≤ n ≤ m). La cola está vacía cuando n = 0 y llena cuando n = m. Otro entero, que designamos por fr, nos indica donde está situado el frente de la cola, es decir, el primer elemento a tratar. Para no perdernos, veamos un ejemplo. Tomemos m = 5, n = 3, fr = 0. En este caso, la cola es la siguiente:

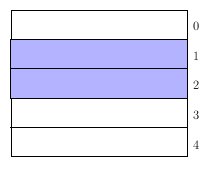
y por consiguiente, ahora es n = 2, fr = 1. Es decir, cada vez que extraigamos un elemento, el frente avanza una unidad módulo m y n se decrementa en 1.
Veamos ahora las operaciones a realizar:
Insertar un elemento en la cola
El algoritmo es:

Extraer un elemento de la cola
El algoritmo es:

Para aclarar las ideas, seguimos con el ejemplo anterior. La situación había quedado como n = 2, fr = 1, es decir:

i = (fr + n) % m → i = (1 + 2) % 5 = 3 % 5 = 3
es decir, copiamos el dato a la posición i = 3 e incrementamos n, con lo que n = 3, y la cola queda como:

i = (fr + n) % m → i = (1 + 3) % 5 = 4 % 5 = 4
es decir, copiamos el dato a la posición i = 4 e incrementamos n, con lo que n = 4, y la cola queda como:

Extraemos ahora. Siguiendo el algoritmo, sea x el elemento situado en la posición 1:
fr = (fr + 1) % m → fr = (1 + 1) % 5 = 2 % 5 = 2
y decrementamos n, con lo que n = 3, y la cola queda como:

Finalmente, volvemos a insertar un elemento más. Otra vez:
i = (fr + n) % m → i = (2 + 3) % 5 = 5 % 5 = 0
es decir, copiamos el dato a la posición i = 0 e incrementamos n, con lo que n = 4, y la cola queda como:

Observemos, que no es necesario correr los elementos, los cuales se encuentran ocupando posiciones consecutivas, naturalmente, módulo m. La programación se ha complicado un poco, pero hemos ganado en eficiencia.
Definición de una cola circular en C
Es conveniente separar los datos de los índices, así que la definición de una cola es la siguiente:
struct cola {
int fr; /* el frente de la cola */
int n; /* número de elementos de la cola */
int nmax; /* número máximo de elementos de la cola */
struct dato *p;
};
donde en algún lugar hay que definir la estructura dato. Si cambiamos esta última, la cola también cambia y no hay que hacer cambios en la estructura. Las variables están claras, salvo que nmax es la m de los ejemplos anteriores. Falta, para completar el estudio, el inicializar una cola, lo cual se hace con una llamada a malloc, en concreto, si definimos:
struct cola x;
y nmax es el número máximo de elementos que contendrá x, entonces:
void inicializacola(struct cola *x, int nmax) {
struct dato *q; /* auxiliar */
q = (struct dato *)malloc(nmax * sizeof(struct dato));
x->fr = 0;
x->n = 0;
x->nmax = nmax;
x->p = q;
}
con lo cual disponemos de nmax estructuras dato:
x->p[0], x->p[1], ... , x->p[nmax - 1]
Manejo del programa
Descargue colas.tgz y siga las siguientes instrucciones:
-
Abra un emulador de terminal, por ejemplo xterm, y
sitúese en un directorio donde tenga permiso de escritura para
practicar. Descomprima aquí el archivo descargado, introduciendo:
tar zxvf colas.tgz
con lo que obtendrá el programa fuente colas.c y tres archivos de datos que son:
diezprimeros.txt, datos.txt y grande.txt
que contienen 10, 20 y 64 personas respectivamente. -
Compile colas.c, para lo cual, introduzca:
cc colas.c -o colas
No debe tener problemas con la compilación, pues solamente se han utilizado funciones estándar del lenguaje C.
Este programa admite 2 argumentos, que son el archivo de datos y el ancho de pantalla. Si no introduce argumentos, por defecto, toma como archivo de datos diezprimeros.txt y el ancho de pantalla en 80 caracteres.
Los archivos de datos son una simulación aleatoria de nombres de personas, dni y fecha de nacimiento.
-
Ejecute el programa introduciendo:
./colas
Inmediatamente aparecen dos líneas de información que muestran que el archivo de datos es diezprimeros.txt y el ancho de pantalla a 80. De momento no podrá insertar nada, ya que la cola está llena. No obstante, inténtelo: entre 1 y enter. Efectivamente, no puede ser. Para mostrar la cola, pulse 3 y enter. Aparecerán los datos. El campo índice muestra el índice del lugar donde están los datos. Si quiere ver la cola gráficamente, entre 4 y enter.
Tenga cuidado con las entradas, ya que al utilizar la librería estándar, si tiene que introducir un número e introduce una letra, el cuelgue está garantizado. Todo esto podría evitarse, pero no, lo que pretendo es que entienda el algoritmo, y por tanto, los adornos no se han tenido en cuenta.
Extraiga e inserte elementos, y vaya observando el frente para comprenderlo. Una advertencia más: cuando inserte en la cola y le pida el nombre, no introduza más de 20 caracteres y sin espacios en blanco. En la fecha de nacimiento, escríbala en la forma dia/mes/año, escribiendo los separadores. Por ejemplo, la entrada:
15/2/1980
es válida. -
Si quiere cambiar el archivo de texto o el ancho de pantalla, ejecute
el programa de la siguiente forma:
./colas archivo-de-datos ancho-de-pantalla
Algunos ejemplos son:./colas datos.txt 120 ./colas grande.txt 100
Finalmente, si encuentra algún error, comuníquelo para su corrección.