Diagramas de flujo en LaTeX

Resumen

Este artículo le muestra cómo hacer un diagrama de flujo en LaTeX. Los diagramas son importantes para clarificar los programas, de hecho, cuando estos últimos se vuelven complejos, los primeros aclaran el procedimiento a seguir, aportando además una buena documentación que nos ayudará a comprender una vez que el tiempo ha pasado y olvidamos lo que hicimos.

Como es evidente, para comprender lo que sigue, el lector debe tener conocimientos de LaTeX y de programación.

Un diagrama de flujo tiene que ser independiente de cualquier lenguaje de programación, en otras palabras, debe valer para todos. No obstante, cuando queramos comprobar el funcionamiento, ha de transcribirse a un determinado lenguaje. Como el que habitualmente utilizo es Lisp, concretamente Common Lisp, se proporcionan los fuentes para que Vd. haga lo mismo.

Por último, para los diagramas he utilizado pstricks, seguramente, el mejor paquete gráfico para LaTeX.

Ejemplos pstricks

El conjunto de utilidades pstricks es muy extenso. Posee muchos subconjuntos, algunos de los cuales son complejos. Nos centraremos en lo que necesitamos para conseguir lo que queremos, que es hacer un diagrama de flujo aceptable. Si el lector, animado con lo que aquí aprende, desea ampliar conocimientos, descargue el manual y estúdielo. Vale la pena.

Comencemos con el ejemplo más simple. En el preámbulo del documento, escriba:

\usepackage{pstricks,pst-node}
      

y en el documento, lo siguiente:

\begin{center}
  \begin{psmatrix}
    & [name=nodo1,mnode=circle] Nodo 1 \\
    & [name=nodo2,mnode=circle] Nodo 2 \\
    \ncline{->}{nodo1}{nodo2}
  \end{psmatrix}
\end{center}
      

Después de procesar el texto, el resultado es:

Hemos utilizado el entorno psmatrix, que es como array, pero vale en modo texto y matemático. Para la mayoría de diagramas de flujo, con tres columnas es suficiente. En el ejemplo anterior, hemos utilizado dos.

En la primera fila, creamos un nodo circular (mnode = circle) de nombre nodo1 (name = nodo1) y cuyo texto es Nodo 1. Es muy importante que a cada nodo se le dé un nombre, el cual debe ser alfanumérico, y como es habitual, comenzando por una letra, ya que después utilizaremos ese nombre para hacer las conexiones.

Igual cosa hemos hecho en la segunda fila. Por último, conectamos los nodos con ncline (node connection line, en español, línea de conexión de nodos). El argumento {->} añade una punta de flecha al final del nodo 2.

Veamos ahora un segundo ejemplo un poco más complicado, en concreto, un test, que corresponde en programación a la terna (if, then, else). Entramos lo siguiente:

\begin{center}
  \begin{psmatrix}[rowsep=1cm,colsep=1cm]
    & [name=test,mnode=dia] ¿test?
    & [name=testn] \psframebox{\parbox{4cm}{\centering Cosas que hacer cuando el test es falso}} \\
    & [name=tests] \psframebox{\parbox{4.2cm}{\centering Cosas que hacer cuando el test es cierto}} \\
    & [name=restoprog] \psframebox{\parbox{3cm}{\centering Resto del programa}} \\

    \ncline{->}{test}{testn}\naput{No}
    \ncline{->}{test}{tests}\naput{Sí}
    \ncline{->}{tests}{restoprog}
    \ncangle[angleA=-90]{->}{testn}{restoprog}
  \end{psmatrix}
\end{center}
      

Obtenemos:

La orden \naput coloca el texto en la línea que une los dos nodos. Más complicada es la orden \ncangle. Como \ncline, conecta dos nodos, pero el cómo lo hace es controlado por cuatro variables que son angleA, armA, angleB y armB. En concreto:

• angleA. Es el ángulo en grados sexagesimales que forma el segmento que sale del nodo primero con la horizontal. A efectos prácticos, los siguientes ángulos serán los más habituales:
  • angleA = 0 (defecto) → Este
  • angleA = 90 → Norte
  • angleA = 180 → Oeste
  • angleA = -90 → Sur
• armA (arm es brazo en inglés), es decir, la longitud del segmento que sale del nodo primero. No debe definirse con la orden \ncangle.
• angleB. Igual que angleA pero para el nodo destino, es decir, es el ángulo en grados sexagesimales que forma el segmento que llega al nodo segundo con la horizontal.
• armB. Igual que armA pero para el nodo destino, es decir, la longitud del segmento que llega al nodo segundo.

Concluímos lo que hace la orden \ncangle: definidas las variables angleA, angleB y armB, ajusta armA de forma que el segmento intermedio sea perpendicular al que sale del primero. En general, dibuja tres segmentos, pero como no ha hecho falta en el ejemplo anterior, solo ha dibujado dos.

Introduzca la siguiente modificación:

\begin{center}
  \begin{psmatrix}[rowsep=1cm,colsep=1cm]
    & [name=test,mnode=dia] ¿test?
    & [name=testn] \psframebox{\parbox{4cm}{\centering Cosas que hacer cuando el test es falso}} \\
    & [name=tests] \psframebox{\parbox{4.2cm}{\centering Cosas que hacer cuando el test es cierto}} \\
    & [name=restoprog] \psframebox{\parbox{3cm}{\centering Resto del programa}} \\

    \ncline{->}{test}{testn}\naput{No}
    \ncline{->}{test}{tests}\naput{Sí}
    \ncline{->}{tests}{restoprog}
    \ncangle[armB=7cm]{->}{testn}{restoprog}
  \end{psmatrix}
\end{center}
      

cuya salida es:

Para que todo quede claro, la siguiente imagen ha sido tomada del manual:

Si le gustan los efectos especiales, introduzca:

\begin{center}
  \begin{psmatrix}[rowsep=1cm,colsep=1cm]
    & [name=test,mnode=dia] ¿test?
    & [name=testn] \psframebox{\parbox{4cm}{\centering Cosas que hacer cuando el test es falso}} \\
    & [name=tests] \psframebox{\parbox{4.2cm}{\centering Cosas que hacer cuando el test es cierto}} \\
    & [name=restoprog] \psframebox{\parbox{3cm}{\centering Resto del programa}} \\

    \ncline{->}{test}{testn}\naput{No}
    \ncline{->}{test}{tests}\naput{Sí}
    \ncline{->}{tests}{restoprog}
    \ncangle[armB=7cm,linearc=0.5]{->}{testn}{restoprog}
  \end{psmatrix}
\end{center}
      

y obtendrá:

Otro ejemplo más: un bucle con su test. Introduzca:

\begin{psmatrix}[rowsep=1cm,colsep=1cm]
  & [name=comienzo,mnode=oval] \parbox{5cm}{\centering Una prueba de diagrama y conexiones} \\
  & [name=buclea,mnode=circle] A \\
  & [name=testbuca,mnode=dia] ¿test?
  & [name=testn] \psframebox{\parbox{4cm}{\centering Cosas que hacer cuando el test es falso}} \\
  & [name=tests] \psframebox{\parbox{4.2cm}{\centering Cosas que hacer cuando el test es cierto}} \\
  & [name=restoprog] \psframebox{\parbox{3cm}{\centering Resto del programa}} \\

  \ncline{->}{comienzo}{buclea}
  \ncline{->}{buclea}{testbuca}
  \ncline{->}{testbuca}{tests}\naput{Sí}
  \ncline{->}{testbuca}{testn}\naput{No}
  \ncline{->}{tests}{restoprog}

  \ncangle[angleA=-90,linearc=0.2]{->}{testn}{restoprog}
  \ncangle[angleA=180,angleB=180,armB=3cm,linearc=0.2]{->}{restoprog}{buclea}
\end{psmatrix}
      

para obtener:

Una última variante del diagrama anterior. Introduzca:

\begin{psmatrix}[rowsep=1cm,colsep=1cm]
  & [name=comienzo,mnode=oval] \parbox{5cm}{\centering Una prueba de diagrama y conexiones} \\
  & [name=buclea,mnode=circle] A \\
  & [name=testbuca,mnode=dia] ¿test?
  & [name=testn] \psframebox{\parbox{4cm}{\centering Cosas que hacer cuando el test es falso}} \\
  & [name=tests] \psframebox{\parbox{4.2cm}{\centering Cosas que hacer cuando el test es cierto}} \\
  & [name=restoprog] \psframebox{\parbox{5cm}{\centering Cuerpo y actualización del bucle}} \\

  \ncline{->}{comienzo}{buclea}
  \ncline{->}{buclea}{testbuca}
  \ncline{->}{testbuca}{tests}\naput{Sí}
  \ncline{->}{testbuca}{testn}\naput{No}
  \ncline{->}{tests}{restoprog}

  \ncangle[angleA=-90,linearc=0.2]{->}{testn}{restoprog}
  \ncangles[angleA=-90,armA=1cm,angleB=180,armB=4cm,linearc=0.2]{->}{restoprog}{buclea}
\end{psmatrix}
      

Le saldrá:

En éste ejemplo hemos utilizado la orden \ncangles, idéntica a \ncangle, pero que dibuja cuatro segmentos. Las variables de control angleA,armA,angleB,armB han sido ya explicadas antes.

Veamos ahora ejemplos concretos de programación.

Ejemplos

Algoritmo de Euclides para el cálculo del máximo común divisor de dos números

De todos los algoritmos, el de Euclides es el número 1, el que encabeza la lista, por las siguientes razones: es bello, breve y elegante. Consiste en lo siguiente: sean a,b dos números enteros positivos, es decir, a,b ≥ 0. Queremos hallar su máximo común divisor, es decir, de todos los divisores comunes a ambos números, el más grande. Lo escribiremos como mcd(a,b) (léase, máximo común divisor de a y b).

Si b = 0, entonces, no hay nada que hacer, directamente, mcd(a,0) = a. Lo mismo ocurre si a = 0, pues entonces, mcd(0,b) = b. Supongamos pues que a,b > 0. Con la tabla:

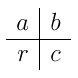
expresamos otro algoritmo muy importante, el de la división entera, es decir, al dividir a entre b, obtenemos un cociente c y un resto r con:

a = b × c + r, 0 ≤ r < b

El algoritmo de Euclides dice que

mcd(a,b) = mcd(b,r)

Observemos como el cociente c no interviene en el algoritmo. Todos los lenguajes de programación proporcionan una forma de calcular el resto de la división entre dos enteros. Adoptaré la notación funcional mod (módulo), es decir:

r = mod(a,b) = resto de la división entre a y b

En fin, en el documento, escriba:

\begin{center}
  \begin{psmatrix}[rowsep=1cm,colsep=1cm]
    & [name=comienzo,mnode=oval] \parbox{6cm}{\centering Calcula el máximo común divisor de dos enteros $a$ y $b$, siendo $a,b\geq 0$} \\
    & [name=combuca,mnode=circle] A \\
    & [name=testbuca,mnode=dia] ¿Es $b = 0$? &
    [name=finprog] \psframebox{\parbox{4cm}{\centering Hemos acabado\newline Retorna $a$}} \\
    & [name=recurre] \psframebox{\parbox{4cm}{\centering
        Sea $r=\text{mod}(a,b)$ \newline
        Hacer $a = b$, $b=r$}} \\
    
    \ncline{->}{comienzo}{combuca}
    \ncline{->}{combuca}{testbuca}
    \ncline{->}{testbuca}{finprog}\naput{Sí}
    \ncline{->}{testbuca}{recurre}\naput{No}
    \ncangle[angleA=180,armB=3cm,angleB=180]{->}{recurre}{combuca}
  \end{psmatrix}
\end{center}
      

Y obtendrá:

Comenzamos con el par (a,b). En la siguiente iteración (b,r), con 0 ≤ r < b. En la siguiente (r,r'), con 0 ≤ r' < r < b. En otras palabras, en cada iteración el resto (segundo argumento) se hace más pequeño, pero manteniéndose positivo, luego llegará un momento en que será 0. Cuando esto ocurra, el control Sí de ¿Es b = 0? asegura la terminación del bucle y del algoritmo.

En Common Lisp, la versión iterativa del algoritmo es:

(defun mcd (a b)
  (let (
	(r 0)
	)
    (loop while (> b 0) do
	  (setf r (mod a b))
	  (setf a b)
	  (setf b r)
	  )
    a
    )
  )
      

y la versión recursiva:

(defun mcdr (a b)
  (if (= b 0) a (mcdr b (mod a b))))
      

Como siempre, la versión recursiva es mucho más elegante. ¡Una única línea de programación!, razón por la cual es el líder de los algoritmos, proporciona mucho con muy poco.

Juego para adivinar un número

Ahora vamos a hacer un diagrama más largo, correspondiente a un pequeño juego. Éste consiste en lo siguiente: el ordenador elige al azar un número, llamémosle e, entre 1 y 1000 y se trata de que lo adivinemos. Para ello, vamos introduciendo números hasta conseguirlo. Sea a el número introducido. El programa debe informarnos con las tres siguientes reglas básicas:

1. a = e → ¡Acertaste!
2. a > e → ¡Alto!
3. a < e → ¡Bajo!

Si jugamos bien, con el método de la bisección, debemos adivinar el número como máximo en 10 intentos, pues 2¹⁰ = 1024 > 1000. No obstante, para aumentar el interés del juego, vamos a animarlo añadiendo unas cuantas reglas más. Sea Δ = |a - e|, es decir, el valor absoluto del error absoluto. Las reglas a programar son:

• 1 ≤ Δ ≤ 5 → ¡Te estás quemando!
• 6 ≤ Δ ≤ 10 → ¡Muy caliente!
• 11 ≤ Δ ≤ 20 → ¡Caliente!
• 21 ≤ Δ ≤ 50 → ¡Frío!
• Δ ≥ 51 → ¡Muy frío!

El texto del diagrama es:

\begin{psmatrix}[rowsep=0.4cm]
  & [name=comienzo,mnode=oval] \parbox{5cm}{\centering Adivinar un número $e$ entre \texttt{inf} y \texttt{sup}} \\
  & [name=nint] \psframebox{\parbox{2cm}{\centering
      $\text{nint} = 1$}} \\
  & [name=combuca,mnode=circle] A \\
  & [name=introduce] \psframebox{\parbox{5cm}{\centering
      Introducir un número \texttt{a} entre \texttt{inf} y \texttt{sup}\newline (\texttt{s} para salir)}} \\
  [name=salidan] \psframebox{\parbox{2cm}{\centering Salir}}
  & [name=testbuca,mnode=dia] ¿Es s o S? \\
  & [name=entcorrecta,mnode=dia]\parbox{3cm}{\centering ¿Es $a\in\enteros$ y\newline \texttt{inf} $\leq a\leq$\texttt{sup}?} &
  [name=errorent] \psframebox{\parbox{2cm}{\centering Error}} \\
  & [name=esigual,mnode=dia] ¿Es $a=e$? &
  [name=acerto] \psframebox{\parbox{2cm}{\centering ¡Acertaste!\newline Salir}} \\
  & [name=esmayor,mnode=dia] ¿Es $a > e$? &
  [name=esalto] \psframebox{\parbox{2cm}{\centering ¡Es alto!}} \\
  & [name=esbajo] \psframebox{\parbox{2cm}{\centering ¡Es bajo!}} \\
  & [name=buscalo] \psframebox{\parbox{4cm}{\centering Búscalo en la lista de rangos}} \\
  & [name=sencontro,mnode=dia] ¿Se encontró? &
  [name=errorint] \psframebox{\parbox{3cm}{\centering Error interno\newline Salir}} \\
  & [name=actualiza] \psframebox{\parbox{4cm}{\centering
      Imprimir el mensaje\newline $\text{nint}=\text{nint}+1$}} \\

  \ncline{->}{comienzo}{nint}
  \ncline{->}{nint}{combuca}
  \ncline{->}{combuca}{introduce}
  \ncline{->}{introduce}{testbuca}
  \ncline{->}{testbuca}{salidan}\naput{Sí}
  \ncline{->}{testbuca}{entcorrecta}\naput{No}
  \ncline{->}{entcorrecta}{errorent}\naput{No}
  \ncangle[angleA=90,angleB=0]{->}{errorent}{combuca}
  \ncline{->}{entcorrecta}{esigual}\naput{Sí}
  \ncline{->}{esigual}{acerto}\naput{Sí}
  \ncline{->}{esigual}{esmayor}\naput{No}
  \ncline{->}{esmayor}{esalto}\naput{Sí}
  \ncline{->}{esmayor}{esbajo}\naput{No}
  \ncline{->}{esbajo}{buscalo}
  \ncangle[angleA=-90,angleB=0]{->}{esalto}{buscalo}
  \ncline{->}{buscalo}{sencontro}
  \ncline{->}{sencontro}{errorint}\naput{No}
  \ncline{->}{sencontro}{actualiza}\naput{Sí}
  \ncangles[armA=1cm,angleA=-90,armB=7.5cm,angleB=180]{->}{actualiza}{combuca}
\end{psmatrix}
      

y el diagrama es:

En vez de utilizar conexiones tan largas como la que se ve desde la parte inferior hasta el comienzo del bucle A, puede usar conectores, como el del siguiente diagrama, modificado del anterior:

cuyo texto es:

\begin{psmatrix}[rowsep=0.4cm]
  & [name=comienzo,mnode=oval] \parbox{5cm}{\centering Adivinar un número $e$ entre \texttt{inf} y \texttt{sup}} \\
  & [name=nint] \psframebox{\parbox{2cm}{\centering
      $\text{nint} = 1$}} \\
  & [name=combuca,mnode=circle] A \\
  & [name=introduce] \psframebox{\parbox{5cm}{\centering
      Introducir un número \texttt{a} entre \texttt{inf} y \texttt{sup}\newline (\texttt{s} para salir)}} \\
  [name=salidan] \psframebox{\parbox{2cm}{\centering Salir}}
  & [name=testbuca,mnode=dia] ¿Es s o S? \\
  & [name=entcorrecta,mnode=dia]\parbox{3cm}{\centering ¿Es $a\in\enteros$ y\newline \texttt{inf} $\leq a\leq$\texttt{sup}?} &
  [name=errorent] \psframebox{\parbox{2cm}{\centering Error}} \\
  & [name=esigual,mnode=dia] ¿Es $a=e$? &
  [name=acerto] \psframebox{\parbox{2cm}{\centering ¡Acertaste!\newline Salir}} \\
  & [name=esmayor,mnode=dia] ¿Es $a > e$? &
  [name=esalto] \psframebox{\parbox{2cm}{\centering ¡Es alto!}} \\
  & [name=esbajo] \psframebox{\parbox{2cm}{\centering ¡Es bajo!}} \\
  & [name=buscalo] \psframebox{\parbox{4cm}{\centering Búscalo en la lista de rangos}} \\
  & [name=sencontro,mnode=dia] ¿Se encontró? &
  [name=errorint] \psframebox{\parbox{3cm}{\centering Error interno\newline Salir}} \\
  [name=combucar,mnode=circle] A
  & [name=actualiza] \psframebox{\parbox{4cm}{\centering
      Imprimir el mensaje\newline $\text{nint}=\text{nint}+1$}} \\

  \ncline{->}{comienzo}{nint}
  \ncline{->}{nint}{combuca}
  \ncline{->}{combuca}{introduce}
  \ncline{->}{introduce}{testbuca}
  \ncline{->}{testbuca}{salidan}\naput{Sí}
  \ncline{->}{testbuca}{entcorrecta}\naput{No}
  \ncline{->}{entcorrecta}{errorent}\naput{No}
  \ncangle[angleA=90,angleB=0]{->}{errorent}{combuca}
  \ncline{->}{entcorrecta}{esigual}\naput{Sí}
  \ncline{->}{esigual}{acerto}\naput{Sí}
  \ncline{->}{esigual}{esmayor}\naput{No}
  \ncline{->}{esmayor}{esalto}\naput{Sí}
  \ncline{->}{esmayor}{esbajo}\naput{No}
  \ncline{->}{esbajo}{buscalo}
  \ncangle[angleA=-90,angleB=0]{->}{esalto}{buscalo}
  \ncline{->}{buscalo}{sencontro}
  \ncline{->}{sencontro}{errorint}\naput{No}
  \ncline{->}{sencontro}{actualiza}\naput{Sí}
  \ncline{->}{actualiza}{combucar}
\end{psmatrix}
      

Descarga y ejecución del programa

Descargue el programa adivina.lsp. Supongamos que lo almacena en el directorio (ahora se llaman carpetas) pruebas. Abra un emulador de terminal, por ejemplo xterm y sitúese en dicho directorio. Cargue el intérprete de Lisp. Yo utilizo clisp, así pues, introduzco:

pedro@servidor2:~/pruebas> clisp
... Información de los mensajes del ntérprete ...
      

Cargo el programa:

[1]> (load "adivina.lsp")
;; Loading file adivina.lsp ...
;; Loaded file adivina.lsp
T
      

y finalmente, juego, introduciendo:

[2]> (juega)
Introduce número [1..1000] (s para salir). Intento no.1: 500
Bajo. Muy frío
Introduce número [1..1000] (s para salir). Intento no.2: 750
Bajo. Muy frío
Introduce número [1..1000] (s para salir). Intento no.3: 875
Bajo. Muy frío
Introduce número [1..1000] (s para salir). Intento no.4: 937
Alto. Te estás quemando
Introduce número [1..1000] (s para salir). Intento no.5: 934
¡Acertaste!. No. de intentos = 5
Nueva partida.
Introduce número [1..1000] (s para salir). Intento no.1: s
Adiós
NIL
      

La función juega tiene un argumento opcional que es el número a adivinar. Está pensado para hacer pruebas de depuración. En la siguiente partida, el número es aleatorio. Veamos un ejemplo:

[3]> (juega 215)
Introduce número [1..1000] (s para salir). Intento no.1: 210
Bajo. Te estás quemando
Introduce número [1..1000] (s para salir). Intento no.2: 216
Alto. Te estás quemando
Introduce número [1..1000] (s para salir). Intento no.3: 215
¡Acertaste!. No. de intentos = 3
Nueva partida.
Introduce número [1..1000] (s para salir). Intento no.1: 500
Alto. Muy frío
Introduce número [1..1000] (s para salir). Intento no.2: 250
Alto. Muy caliente
Introduce número [1..1000] (s para salir). Intento no.3: 241
Alto. Te estás quemando
Introduce número [1..1000] (s para salir). Intento no.4: 240
¡Acertaste!. No. de intentos = 4
Nueva partida.
Introduce número [1..1000] (s para salir). Intento no.1: 
      

Por último, los diagramas de flujo antes expuestos corresponden a la función Lisp adivina-numero, incluída en el programa fuente.

Contacto

Si desea hacer algún comentario, utilice la siguiente dirección de correo:

Pedro González Ruiz
Fecha de creación: 3 de octubre de 2017
Fecha de la última modificación: 3 de octubre de 2017

ir a la página principal