Listas enlazadas en C

Pedro González Ruiz

Listas

Una lista es una estructura dinámica de datos. Cada objeto de la estructura está formado por los datos junto con un puntero al siguiente objeto. Al manejar punteros, los datos no tienen por qué estar situados en posiciones consecutivas de la memoria, y lo más normal, es que estén dispersos. Debe imaginarse una lista de la siguiente forma:

(O1, O2, ... , On)

O1 es el primer objeto y está constituido por dos partes: los datos que pretendemos almacenar, que simbólicamente llamaremos D1, y un puntero p1 que apuntará al siguiente objeto, en éste caso O2, es decir:

Discusión análoga para O2 y así sucesivamente. El final de la lista es el objeto On, cuyo puntero pn apunta a NULL, es decir, a ningún sitio. De esta forma, podemos saber cual es el final de la lista.

Cada elemento de datos, por ejemplo, el D1 de antes, será una estructura (struct) en el sentido del lenguaje C. Una lista vacía la representaremos de varias formas, que son: ∅ (símbolo matemático del conjunto vacío), NULL o también por (). Técnicamente hablando, una lista l contiene la dirección del primer objeto.

Las listas no tienen problemas para crecer a izquierda, centro o derecha, dependiendo de lo que se pretenda conseguir. La única pega es la memoria disponible. También, las listas engloban a las pilas y colas. En consecuencia, saber manejar bien las listas, implica conocer más cosas.

Si, como consecuencia de la lectura de este artículo, llega a aprender y dominar las listas, y tiene tiempo, debe plantearse estudiar el lenguaje LISP (de LISt Processing, es decir, manejo de listas), que desde mi punto de vista, es el mejor lenguaje de programación de todos los que conozco.

Las listas también pueden estar doblemente enlazadas, es decir, cada objeto, contiene dos punteros, uno de ellos, al siguiente, como antes, y otro, al anterior. De esta forma, puede ir hacia adelante y hacia atrás (vea la siguiente figura):

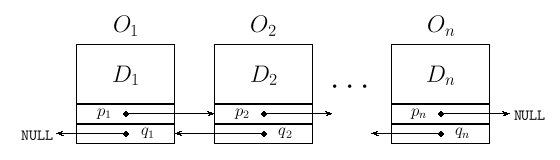
Estas no las vamos a tratar aquí, aunque haciendo pequeñas modificaciones al programa, lo conseguirá sin dificultad.

Definición de lista en C

Según comentamos en el apartado anterior, es conveniente separar los datos de los punteros, así que la definición de lista es la siguiente: 

struct lista { /* lista simple enlazada */
  struct dato datos;
  struct lista *sig;
};

donde en algún lugar hay que definir la estructura dato. Si cambiamos esta última, la lista también cambia y no hay que hacer cambios en ella. Las variables están claras, datos es el objeto D1 comentado antes, y sig es el puntero que apunta al siguiente objeto (el p1 de la figura).

Para inicializar una lista, basta con escribir: 

struct lista *l; /* declaración */
l = NULL; /* inicialización */

Este par de sentencias constituyen la forma de crear una lista vacía, es decir, l = ∅

Operaciones con listas

Calcular la longitud de una lista

es decir, el número de elementos que contiene. El algoritmo no puede ser más simple, inicializamos un contador a cero, y vamos recorriendo la lista, incrementando dicho contador, hasta encontrar el NULL final. En concreto: 

/* Devuelve la longitud de una lista */
int longitudl(struct lista *l) {
  struct lista *p;
  int n;
  n = 0;
  p = l;
  while (p != NULL) {
    ++n;
    p = p->sig;
  }
  return n;
}

Insertar un dato al comienzo de una lista

En concreto, sea x una estructura tipo dato y l = (O1, O2, ... , On) una lista. Después de la operación debe quedar

(x, O1, O2, ... , On)

Para esto, debemos aprender a crear un nuevo nodo, lo cual es una llamada a malloc, en concreto: 

struct lista *creanodo(void) {
  return (struct lista *) malloc(sizeof(struct lista));
}

Una vez visto esto, debemos hacer lo siguiente:

y la función es: 
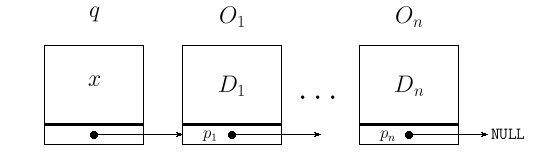
/* Inserta dato al comienzo de la lista (para pilas) */
struct lista *insertacomienzo(struct lista *l, struct dato x) {
  struct lista *q;
  q = creanodo(); /* crea un nuevo nodo */
  q->datos = x; /* copiar los datos */
  q->sig = l;
  l = q;
  return l;
}

Insertar un dato al final de una lista

En concreto, sea x una estructura tipo dato y l = (O1, O2, ... , On) una lista. Después de la operación debe quedar

(O1, O2, ... , On, x)

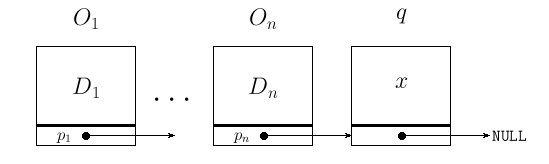
Aquí debemos distinguir si l = ∅, o no. En el primer caso, debe quedar l = (x), y si l ≠ ∅ debemos situarnos en el último y asignar los punteros:

y la función es: 
/* Inserta dato al final de la lista (para colas) */
struct lista *insertafinal(struct lista *l, struct dato x) {
  struct lista *p,*q;
  q = creanodo(); /* crea un nuevo nodo */
  q->datos = x; /* copiar los datos */
  q->sig = NULL;
  if (l == NULL)
    return q;
  /* la lista argumento no es vacía. Situarse en el último */
  p = l;
  while (p->sig != NULL)
    p = p->sig;
  p->sig = q;
  return l;
}

Insertar un dato en una lista ordenada

Se entiende por lista ordenada una lista en la que se ha definido una función de ordenación. Para aclarar las cosas, volvemos a nuestra imagen de lista:

l = (O1, O2, ... , On)

Sabemos que cada objeto O está formado por dos partes: el dato D y el puntero sig, con lo cual tenemos también la sucesión de los datos:

(D1, D2, ... , Dn)

La lista está ordenada cuando tenemos definida una función binaria f sobre los datos de forma que (D, E son estructuras tipo dato):

D < E ⇔ f(D,E) = -1
D = E ⇔ f(D,E) = 0
D > E ⇔ f(D,E) = 1

Como es evidente, los valores -1,0,1 son totalmente arbitrarios y podrían sustituirse por cualquier otros. Lo hacemos así por analogía con los valores de retorno de algunas funciones del lenguaje C.

Cuando se haya definido una función de ordenación sobre una lista, diremos que la lista está ordenada, y escribiremos:

D1 ≤ D2 ≤ … ≤ Dn

o también:

O1 ≤ O2 ≤ … ≤ On

Veamos algunos ejemplos:

En fin, debe ya resultar evidente lo que pretendemos, sea x una estructura tipo dato y l = (O1, O2, ... , On) una lista ordenada, es decir:

O1 ≤ O2 ≤ … ≤ On

queremos insertar x en l de forma que la lista resultante esté también ordenada. Un argumento de la función es la función de ordenación, la cual será un puntero a función, de forma que cambiando esta función, la lista pueda ordenarse por criterios distintos. El algoritmo es sencillo, pero exige una búsqueda previa, en concreto:

  1. Si la lista l es vacía, entonces l = (x).

  2. Si no, es decir, si la lista no es vacía, recorremos la lista hasta que encontremos el sitio adecuado para insertar el dato, concretamente, cuando x ≤ D, siendo D el dato actual. Para este apartado, necesitamos ir apuntando el nodo anterior, para hacer los enlaces correctamente. También necesitamos un indicador para parar la búsqueda, cuando se encuentre el sitio.

  3. Por último, insertar el dato en ese lugar.

Veamos un ejemplo aclaratorio, y para simplificar, imaginemos un orden numérico sobre la lista, la cual se representará por sus valores. Sea l = (7, 15, 28), y el dato a insertar x = 19. Recorremos la lista hasta que x ≤ D. Como 19 > 7 y 19 > 15, hay que parar en el tercer elemento, ya que 19 ≤ 28. En este punto, el nodo anterior ant es 15 y el nodo actual es D = p = 28, y si es q el nodo correspondiente a (19), entonces, antes de insertar:

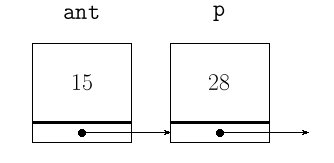
Insertamos con las siguientes instrucciones: 
ant->sig = q;
q->sig = p;
Es decir:

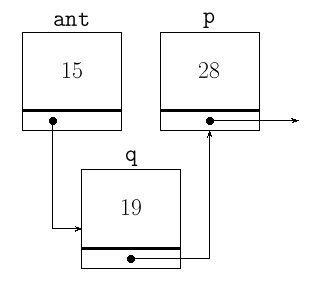
El algoritmo falla cuando no hay anterior, es decir, cuando ant = NULL. Cuando esto ocurre, la inserción es al comienzo, cuestión ya tratada en un apartado anterior.

Observe que el algoritmo anterior también funciona cuando p = NULL, es decir, cuando el objeto a insertar es al final de la lista. En este caso, las sentencias: 

ant->sig = q;
q->sig = p;
se convierten en: 
ant->sig = q;
q->sig = NULL;
lo cual es correcto.

Finalmente, la función de inserción es: 

/*
 Inserta un dato en una lista ordenada.
 La nueva lista debe quedar ordenada
 f es la función de ordenación
*/
struct lista *insertaordenado(struct lista *l, struct dato x, int (*f)(struct dato a, struct dato b)) {
  struct lista *p,*q,*ant;
  int ind;
  q = creanodo(); /* crea un nuevo nodo */
  q->datos = x; /* copiar los datos */
  q->sig = NULL; /* por defecto, puede cambiar */
  if (l == NULL) {
    l = q;
    return l;
  }
  /* la lista no es nula */
  ant = NULL;
  p = l;
  ind = 0;
  while (p != NULL && ind == 0) {
    if ((*f)(x,p->datos) <= 0) /* aquí hay que insertar */
      ind = 1;
    else {
      ant = p;
      p = p->sig;
    }
  }
  if (ant == NULL) { /* inserción al comienzo */
    q->sig = l;
    l = q;
  } else { /* inserción en medio o al final */
    ant->sig = q;
    q->sig = p;
  }
  return l;
}

Eliminar un objeto de la lista

En concreto, l = (O1, O2, ... , On) una lista y x una estructura tipo dato, objeto que queremos borrar de la lista. Vamos a utilizar un procedimiento recursivo, en concreto:

La función de borrado es: 
struct lista *elimina(struct lista *p, struct dato x, int (*f)(struct dato a, struct dato b)) {
  int cond;
  if (p == NULL) /* no hay nada que borrar */
    return p;
  /* compara el dato */
  cond = (*f)(x,p->datos);
  if (cond == 0) { /* encontrado! */
    struct lista *q;
    q = p->sig;
    free(p); /* libera la memoria y hemos perdido el enlace, por eso se guarda en q */
    p = q; /* restaurar p al nuevo valor */
  } else /* no encontrado */
    p->sig = elimina(p->sig,x,f); /* recurre */
    return p;
  }

Las versiones recursivas siempre son más sencillas y elegantes que sus equivalentes iterativas. Un ejercicio interesante es programar la función anterior en forma iterativa.

Anular una lista

En concreto, sea l = (O1, O2, ... , On) una lista. Queremos empezar de nuevo, haciendo que l = NULL. No basta con la ingenua instrucción: 

l = NULL;

pues entonces, toda la memoria que le hemos pedido al sistema operativo se pierde para siempre. Por consiguiente, hay que devolver la memoria utilizada, con la siguiente función: 

/* anula una lista liberando la memoria */
struct lista *anulalista(struct lista *l) {
  struct lista *p,*q;
  p = l;
  while (p != NULL) {
    q = p->sig; /* para no perder el nodo */
    free(p);
    p = q;
  }
  return NULL;
}
y, por tanto, basta con escribir: 
l = anulalista(l);
para que l sea la lista vacía.

Manejo del programa

Descargue listas.tgz y siga las siguientes instrucciones: Finalmente, si encuentra algún error, comuniquémelo para su corrección.

Pilas y colas

Como ejemplo de aplicación de listas, los dos programas pilas.c y colas.c, incluidos en el paquete, son pequeñas variaciones del principal listas.c, salvo que en las colas, la inserción de elementos es al final, y en las pilas, al principio. En ambos casos, las extracciones son al principio, con la función: 

/* Extrae dato al comienzo de la lista (para pilas y colas) */
struct lista *pop(struct lista *l, struct dato *x) {
  if (l != NULL) { /* no hacer nada si l es nula */
    struct lista *p,*q;
    p = l;
    q = p->sig; /* para no perder el enlace */
    *x = p->datos; /* copiar el dato */
    free(p); /* libera memoria */
    l = q;
    return l;
  }
}
El uso de ambos programas es idéntico al de listas.

Contacto

Si desea hacer algún comentario, utilice la siguiente dirección de correo:

Pedro González Ruiz
Fecha de creación: 26 de junio de 2010
Fecha de la última modificación: 25 de octubre de 2015

ir a la página principal