Separación covid 19

Pedro González Ruiz

Introducción

Como consecuencia de los efectos del covid 19, las autoridades sanitarias aconsejan mantener una separación entre personas de 1.5 m., ya que parece ser que con esta distancia se evita el contagio.

Para simplificar, llamaremos d a ésta distancia, es decir, d=1.5 m. Si más adelante éste número cambia, no afectará al contenido, y todo seguirá siendo válido sin más que cambiar d por el nuevo valor.

Esto da origen al siguiente problema: en un terreno rectangular dado, ¿cuál es la mejor forma de distribuir un conjunto de objetos de forma que se mantenga entre ellos una separación de al menos d?.

En otras palabras, pretendemos maximizar el número de objetos a colocar en ella, pero siempre con la condición de que la separación entre ellos sea d al menos.

Como es evidente, dentro del significado de objetos, se incluye el de persona o cualquier otra cosa. El problema planteado es muy general y aquí solamente vamos a tratar de triángulos y cuadrados.

Resultados previos

Triángulo equilátero

Consideremos un triángulo equilátero de lado d, y sea h la altura.

Tenemos:

Funciones techo y suelo

Si x es un número real, por definición, el techo de x, escrito como ⌈x⌉, es el menor entero ≥ x, es decir, el entero más cercano a x por exceso. Por ejemplo:

No se debe confundir ésta función con su compañera, más popular, la parte entera o suelo de x, escrita como ⌊x⌋, que se define como el mayor entero ≤ x, es decir, el entero más cercano a x por defecto. Por ejemplo:

De la definición se deduce inmediatamente que si x es entero, es decir, x∈ℤ, es

⌈x⌉ = ⌊x⌋ = x

pero si x∉ℤ, la igualdad anterior no es cierta, de hecho, si z es la función característica de los enteros, es decir

entonces

⌈x⌉ - ⌊x⌋ = 1 - z(x)

Otra propiedad de las funciones suelo y techo es la siguiente: si x∈ℝ, n∈ℤ, entonces:

⌊x + n⌋ = n + ⌊x⌋, ⌈x + n⌉ = n + ⌈x⌉

es decir, los sumandos enteros pueden entrar o salir de la función.

Colocar objetos

Triángulos

Consideremos un retículo como el de la siguiente figura:

Sea m el número de bandas verticales (4 en el dibujo) y n el número de bandas horizontales (3 en el dibujo). Sea N_t(m,n) el número de objetos (representados por puntos gruesos) contenidos en el rectángulo (el subíndice t es por triángulo) md × nh y S_t(m,n) la superficie de dicho rectángulo, es decir:

S_t(m,n) = md · nh = m·n·r·d²

Pretendemos calcular N_t(m,n). En fin:

n = 1. Éste es un caso muy sencillo pues N_t(m,1) = (m + 1) + m = 2m + 1
n = 2. Se ve claramente que N_t(m,2) = anterior + (m + 1) = 3m + 2
n = 3. Ahora N_t(m,3) = anterior + (m) = 4m + 2
Uno más, n = 4. Ahora N_t(m,4) = anterior + (m + 1) = 5m + 3
Otro más, n = 5. Ahora N_t(m,5) = anterior + (m) = 6m + 3

En fin, se ve ya clara la regla, en concreto:

Por ejemplo, en el dibujo:

Cuadrados

Consideremos un retículo como el de la siguiente figura:

Sea m el número de bandas verticales (4 en el dibujo) y n el número de bandas horizontales (3 en el dibujo). Sea N_c(m,n) el número de objetos (representados por puntos gruesos) contenidos en el rectángulo (el subíndice c es por cuadrado) md × nd y S_c(m,n) la superficie de dicho rectángulo, es decir:

S_c(m,n) = md · nd = m · n · d²

No hay que hacer grandes cálculos para ver que N_c(m,n) = (m + 1) × (n + 1), luego (por tenerlo todo junto)

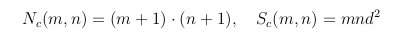
Casos prácticos

Vista ya la parte teórica, veamos algunos ejemplos aclaratorios que muestren la diferencia entre distribuir objetos mediante triángulos o cuadrados.

Para conseguirlo, un buen comienzo serı́a conseguir dos retı́culos con superficies iguales y ver el número de objetos colocados en cada uno de los dos casos. Para simplificar, suponemos que m es el mismo, y por tanto:

Igualando

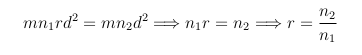
o bien

Esta igualdad es imposible, pues la izquierda es irracional, mientras que la derecha es racional. No obstante, podemos considerar a n₂ / n₁ como una aproximación del irracional cuadrático , con lo que la igualdad anterior debe sustituirse por:

Recordamos ahora un resultado de la teorı́a de números que dice que las convergentes del desarrollo en función continua de un número real α son aproximaciones óptimas de α. En conclusión, desarrollamos el irracional cuadrático en fracción continua (el desarrollo es periódico por ser cuadrático), exponemos las primeras convergentes, y como ejemplos de lo que pretendemos, tomamos los numeradores y denominadores de dichas convergentes. En fin, las primeras convergentes del desarrollo de son:

Tomemos la tercera, es decir, la fracción 6/7. Entonces n₂ = 6, n₁ = 7. Si elegimos m = 10 y d = 1.5, entonces

Vemos que las superficies son prácticamente iguales. Ahora bien

En otras palabras, con prácticamente la misma área, utilizando triángulos, hemos colocado 7 objetos más que con los cuadrados.

Tomemos ahora la cuarta, es decir, la fracción 13/15. Entonces n₂ = 13, n₁ = 15. Si elegimos m = 40 y d = 1.5, es decir, un terreno con una base m × d = 40 × 1.5 = 60 m., entonces:

Otra vez, las superficies son casi idénticas. Ahora bien

En este ejemplo, la diferencia es de 648 − 574 = 74 objetos. En otras palabras, con prácticamente la misma área, utilizando triángulos, hemos colocado 74 objetos más que con los cuadrados.

El lector puede saltar al siguiente apartado. Lo que sigue es para aquellos que tengan conocimientos de fracciones continuas. Mostramos el desarrollo del irracional cuadrático x₀ = y sus primeras convergentes.