Sombrear con Maple la región comprendida entre dos curvas continuas

Pedro González Ruiz

Resumen

Maple no proporciona, al menos que yo sepa, un método para sombrear la región comprendida entre dos curvas continuas. Estas notas muestran cómo conseguirlo. Pero, antes de ello, comencemos dando una definición, que más tarde ampliaremos.

Compacto simple

Se entiende por compacto simple una región S1 del plano definida como

S1≡a≤x≤b , g(x)≤ y ≤ f(x)

donde f y g son funciones continuas en [a,b].

La siguiente figura muestra el aspecto de un compacto simple:

compacto-simple

Debe resultar evidente que los segmentos verticales en x=a, x=b, pueden degenerar en un punto. Para simplificar, un compacto simple es una curva dominante (f), una curva dominada (g) y un intervalo [a,b] de recorrido para la x.

Este tipo de compacto simple lo llamamos de tipo 1.

Si giramos la figura 90° obtenemos un compacto simple de tipo 2, es decir, uno de la forma:

S2≡c≤y≤d , g(y)≤ x ≤ f(y)

La siguiente figura muestra el aspecto de un compacto simple de tipo 2:

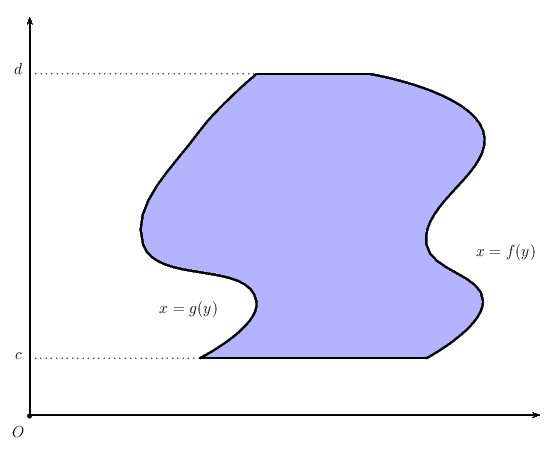
compacto-simple

Debe resultar evidente también que los segmentos horizontales en y=c, y=d, pueden degenerar en un punto.

En las explicaciones que siguen nos limitaremos a los del tipo 1, aunque daremos un ejemplo para los del tipo 2.

Sombreado de un compacto simple tipo 1

Para dibujar un compacto simple tipo 1, necesitamos un procedimiento con al menos 4 argumentos, que son: f,g,a,b. Incluimos un quinto, que es el paso, o separación entre los segmentos verticales de sombreado. Vd., por su cuenta, si lo considera conveniente, puede añadir más argumentos, tales como el color de la sombra, grosor de la línea, etc.

El programa es sombrea1, cuyo listado es: 

sombrea1:=proc(f,g,a,b,paso)
  local z,m,result;
  m:=a;
  result:=[NULL];
  while m<=b do
    z:=plot([m,g(m)+t*(f(m)-g(m)),t=0..1]);
    result:=[op(result),z];
    m:=m+paso;
  od;
  result;
end;

Utilice ahora el método tradicional para insertar éste código en Maple, en concreto, seleccione el texto en el navegador y pulse ctrl + c. Después, sitúese en la ventana de Maple y pulse ctrl + v y listo.

Siga ahora los siguientes pasos dentro de Maple:

  1. Como vamos a utilizar la orden display, debe introducir:

    with(plots)

  2. Previamente al sombreado debe preparar el gráfico sin sombreado para que le quede a su gusto, y a continuación seguir la siguiente secuencia de órdenes (a modo de plantilla): 
    Definir f;
Definir g;
g:=plot(gráfico principal):
s:=sombrea1(f,g,a,b,paso):
display(g,s);
    y listo. Observe la finalización con dos puntos(:) de la asignación de las variables g,s. Debe hacerlo así porque si no aparecerá en pantalla mucha información molesta.
En fin, vista la teoría, veamos ahora un

Ejemplo

Sombrear la región encerrada entre las parábolas:

y=6x-x2 , y=x2-2x

Definimos:

Entramos: 
plot([f(x),g(x)],x=-5..5,-10..10)
La salida es:

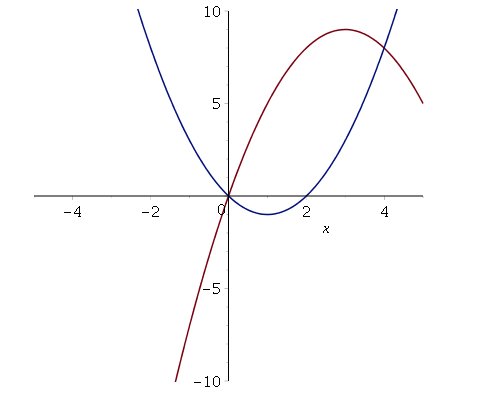
La zona a sombrear corresponde al intervalo [0,4], así que, entramos: 

a := plot([f(x),g(x)],x = -5..5,-10..10):
b := sombrea1(f,g,0,4,0.1):
display(a, b):
y el resultado es:

Si el sombreado lo ve muy espaciado y lo quiere más denso, introduzca: 
b := sombrea1(f,g,0,4,0.01):
	display(a, b):
y el resultado será:

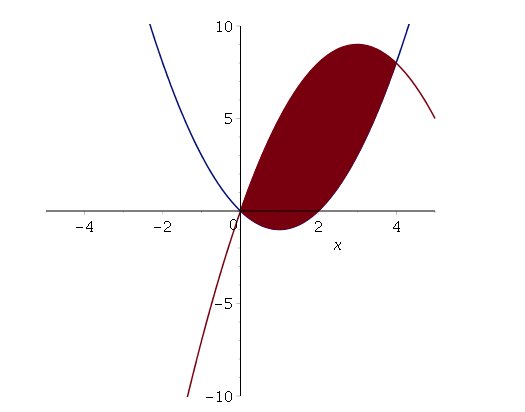
Sombreado de un compacto simple tipo 2

De forma parecida al método anterior, el programa es sombrea2, cuyo listado es: 

sombrea2:=proc(f,g,a,b,paso)
  local z,m,result;
  m:=a;
  result:=[NULL];
  while m<=b do
    z:=plot([g(m)+t*(f(m)-g(m)),m,t=0..1]);
    result:=[op(result),z];
    m:=m+paso;
  od;
  result;
end;

Ejemplo

Sombrear la región encerrada entre la parábola y2=4x y la recta y=2x-4.

Para mostrar la parábola de un tirón la parametrizamos así:

x=t2, y=2t, t∈]-∞,+∞[

y la recta como

x=t, y=2t-4, t∈]-∞,+∞[

Entramos: 
plot({[t**2,2*t,t=-4..4],[t,2*t-4,t=0..5]});
y la salida es:

Despejando la x en ambas curvas:

x=y2/4, x=(y+4)/2

Resolvemos el sistema:

luego c=-2, d=4. Finalmente, introducimos: 
a := plot({[t,2*t-4,t = 0..5],[t^2,2*t,t = -4..4]}):
b := sombrea2(f,g,-2,4,0.1):
display(a,b);
y el resultado es:

Maple 2015

A partir de ésta versión se ha incorporado el procedimiento shadebetween para sombrear un compacto simple tipo 1. Si quiere hacerlo para los de tipo 2, tendrá que descomponer estos en simples tipo 1.

El primer ejemplo quedaría así: 
a := plot([f(x),g(x)],x = -5..5,-10..10):
b := shadebetween(f(x),g(x),x = 0..4,color = "Blue"):
display(a,b)
y el resultado es:

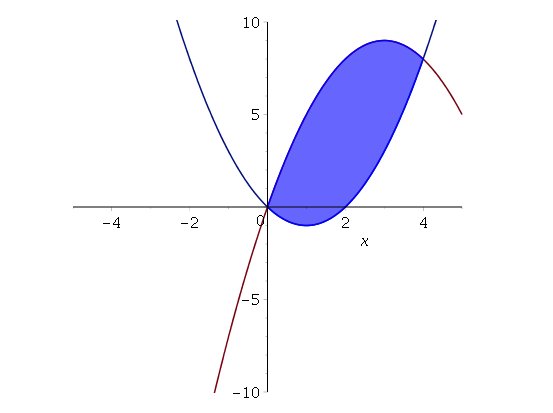
A la vista de los resultados anteriores, el segundo ejemplo, lo hacemos en color naranja, y quedaría como: 
a := plot({[t,2*t-4,t = 0..5],[t^2,2*t,t = -4..4]}):
b := shadebetween(2*sqrt(x),-2*sqrt(x),x = 0..1,color = "Orange"):
c := shadebetween(2*sqrt(x),2*x-4,x = 1..4,color = "Orange"):
display(a,b,c)
Cuya salida es:

Contacto

Si desea hacer algún comentario, utilice la siguiente dirección de correo:

Pedro González Ruiz
Fecha de creación: 2 de julio de 2005
Fecha de la última modificación: 11 de octubre de 2015

ir a la página principal