Método abreviado para obtener la descomposición en fracciones simples de una función racional en un caso particular
Pedro González Ruiz
Introducción y notaciones
Sean p y q polinomios en una indeterminada x, q irreducible sobre ℝ, es decir, de grado 1 o de grado 2 con discriminante negativo, o lo que es lo mismo, sin raíces reales y sea n cualquier número natural. Pretendemos obtener la descomposición de p / qn en fracciones simples de forma sencilla, sin aplicar el método habitual de coeficientes indeterminados.
El grado de un polinomio p lo indicamos como gr(p). La división con resto entre dos polinomios a y b la indicamos como
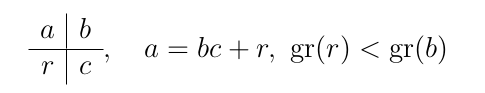
es decir, a es el dividendo, b es el divisor, c es el cociente y r el resto. El discriminante de un polinomio cuadrático ax2+bc+c es Δ=b2-4ac.
Desarrollo
Sea nuestra fracción original p / qn. La regla básica es la siguiente: haciendo la división entre p y q, tenemos
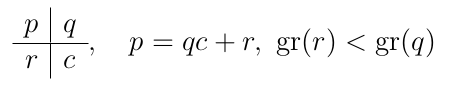
y por tanto
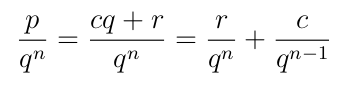

El sumando r / qn está ya desarrollado, puesto que gr(r) < gr(q), y la fracción c / qn-1 es idéntica a la original p / qn, salvo que el grado del cociente c es menor que el grado del original p y que el exponente del denominador es una unidad menos. Siguiendo la recurrencia, obtenemos la descomposición.
Hasta aquí la teoría general. En el documento se muestran las reglas a seguir para varios casos particulares, y en el peor de los casos, cuando q es irreducible de grado 2, todo se reduce a dividir un polinomio entre otro de grado 2, se expone un algoritmo de división para hacer más sencilla la descomposición.