Crear imposiciones
Resumen
Este artículo tiene como objetivo hacer imposiciones a 2,4 y 8 páginas en un papel A4, que es el más corriente. No tiene por qué limitarse al A4, ya que los programas utilizados pueden manejar papeles con otras dimensiones. En la sección siguiente se explica lo que es una imposición. Se adjunta otro artículo en formato pdf donde se dan las explicaciones matemáticas necesarias para justificar los métodos utilizados. Se acompaña también, para hacer prácticas, una agenda, constituida por nombres, teléfonos y direcciones de correo electrónico totalmente aleatoria, en el sentido de que los datos que contiene no corresponden a personas, dominios o teléfonos existentes.
Definición de imposición
La palabra imposición tiene varias acepciones. En éste artículo, se refiere a la utilizada en la construcción de libros mediante cuadernillos. La Real Academia Española la define así:
Composición de cuadrados que separa las planas entre sí, para que, impresas, aparezcan con los márgenes correspondientes.Este significado es difícil de entender, y como definir es también difícil, para lo que se pretende aquí, propongo la siguiente:
Procedimiento para colocar varias páginas pequeñas en otra más grande, de forma que al practicar uno o varios dobleces en ésta última mediante métodos concretos, resulte un cuadernillo cuyas páginas están situadas en el orden natural 1,2,3,...
También es difícil de comprender, pero todo quedará claro cuando hagamos un par de ejemplos. Estos que siguen y todo el artículo está basado en el supuesto de que el papel a utilizar es A4. Han sido preparados para esta medida, así pues, asegúrese de que esta condición se cumple, si no, las cosas no saldrán bien.
Ejemplos de imposiciones
Ejemplo 1. Imposición a 4 páginas
Descargue este documento, el cual contiene 2 páginas y proceda a imprimirlo así:
- Encienda la impresora y retire todo el papel de la bandeja. Deje sólo una hoja en blanco.
-
Imprima la cara primera. Debe obtener una página de 4
rectángulos como la siguiente:

-
Este apartado es el más delicado. Si no le sale bien, tendrá que
volver al punto primero y comenzar de nuevo. Vaya apuntando lo que
va haciendo para no cometer el mismo error dos o más veces.
En fin, ahora queremos imprimir la otra cara del papel. Por tanto, coloque la hoja de forma que la impresora escriba la segunda cara, pero esta colocación la puede hacer de dos formas: directamente o girando la hoja 180 grados. Sólo una de las dos será la correcta. Proceda a ello e imprima la segunda hoja. Debe obtener una página de 4 rectángulos como la siguiente:

- La imposición está bien hecha si la parte trasera del rectángulo 8 es el rectángulo 7, del 1 el 2, del 5 el 6, y del 4 el 3. Si esto es así, magnífico, puede saltar al apartado siguiente, y si no, debe volver a empezar, y recordarle, que en el apartado tercero debe girar la hoja 180 grados para una impresión correcta.
- Si llega hasta aquí, todo va bien. No se desanime, ya queda menos. Ahora vamos a proceder a doblar la hoja para conseguir el cuadernillo. Sitúe la hoja en una mesa, siéntese y colóquela de forma que el rectángulo 2 quede a la vista y en la esquina inferior izquierda. Dóblela perpendicularmente y por la mitad al lado más grande (el de la izquierda), con lo que el rectángulo 3 quedará frente al 2, el 6 frente al 7 y a la vista el 4 y el 5. Doble otra vez por la línea vertical de separación entre el rectángulo 4 y 5, de forma que ambos quedarán enfrentados.
Ejemplo 2. Imposición a 8 páginas
En este ejemplo no vamos a ser tan explícitos como en el anterior. Descargue este documento, el cual contiene 2 páginas y proceda a imprimirlo así:
- Encienda la impresora y retire todo el papel de la bandeja. Deje sólo una hoja en blanco.
-
Imprima la cara primera. Debe obtener una página con 8
rectángulos como la siguiente:

-
Imprima ahora la otra cara del papel. Por tanto, coloque la hoja de
forma que la impresora escriba la segunda cara, pero esta colocación
la puede hacer de dos formas: directamente o girando la hoja 180
grados. Sólo una de las dos será la correcta. Proceda a ello e
imprima la segunda hoja. Debe obtener una página de 8 rectángulos
como la siguiente:
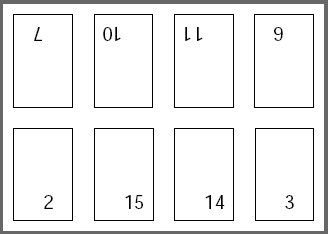
- La imposición está bien hecha si la parte trasera del rectángulo 1 es el rectángulo 2, del 8 el 7, del 16 el 15, ... y del 5 el 6. Si esto es así, magnífico, puede saltar al apartado siguiente, y si no, debe volver a empezar, y recordarle, que en el apartado tercero debe girar la hoja 180 grados para una impresión correcta.
-
Ahora vamos a doblar. Sitúe la hoja en una mesa, siéntese y colóquela
apaisada y de forma que el rectángulo 2 quede a la vista y en la
esquina inferior izquierda. Dóblela perpendicularmente y por la mitad
al lado más grande (el de la base), con lo que el rectángulo 3 quedará
frente al 2, el 6 frente al 7, etc. y a la vista el 4 y el 13 en la
parte inferior.
Gire el papel 90 grados a la derecha de forma que en la base queden el 13 y el 12 y haga lo mismo que en la primera doblez. Una última doblez, haga lo mismo, es decir, gire 90 grados a la derecha y doble otra vez, de forma que el 8 se encuentre enfrente del 9.
Por otro lado, ¡no vaya a creer que a mí me salió a la primera!. Ni mucho menos. Tuve que leer e indagar bastante hasta conseguirlo. Las explicaciones que corren por internet son bastante pobres, y lo que pretendo aquí es clarificar todo esto, debido a su gran utilidad.
Condicionamientos
- Para poder hacer imposiciones, los documentos deben estar en formato postscript, ya que los programas que vamos a utilizar actúan sobre este tipo. Hay excepciones que más adelante se comentarán. Así pues, Vd. por su cuenta, deberá hacer las conversiones oportunas a este formato. No obstante, más adelante se dan algunos consejos de cómo hacerlo.
- El sistema operativo utilizado en todo lo que sigue es Linux, concretamente, y aunque sea irrelevante, Suse 9.3. Si dispone de otra versión más o menos avanzada, no debe tener ningún problema. Si tiene otro, como Windows o Mac, etc. deberá buscar e instalar las herramientas, las cuales son gratuitas.
-
El paquete de programas que vamos a manejar es psutils, que como su nombre indica es un conjunto de utilidades para manipular documentos postscript. Está disponible para Linux y Windows. Utilice los procedimientos habituales de su sistema operativo para instalarlo.
-
Del conjunto de programas que constituyen el paquete, destacamos como principales para nuestro propósito los siguientes:
- Necesita un visor de postcript. Yo utilizo gv, aunque hay otros como okular (visor de documentos del entorno KDE).
pstops, psbook, psnup
Conversiones postscript
-
De pdf a postscript. Utilice el programa pdf2ps. La sintaxis es muy sencilla, en concreto, si el nombre de su documento pdf es, por ejemplo, prueba.pdf, introduciendo:
$ pdf2ps prueba.pdf
obtendrá otro archivo de nombre prueba.ps en el mismo directorio, con lo cual habrá logrado la conversión. -
De LaTeX a postscript. Procese el (los)
archivo(s) .tex y obtenga el .dvi
correspondiente. Supongamos que es
prueba.dvi. Introduzca:
$ dvips -o prueba.ps prueba.dvi
obtendrá otro archivo de nombre prueba.ps en el mismo directorio. -
De Microsoft Word
a postscript. Supongamos que el documento Word
es prueba.doc. Ábralo con Libreoffice
writer y a continuación:
Archivo Exportar en formato PDF..
El resultado de la exportación es prueba.pdf. A continuación siga el procedimiento comentado en el punto primero de esta sección. -
De postscript a pdf. Utilice el programa
ps2pdf. La sintaxis es muy sencilla, en concreto, si
el nombre de su documento postscript es, por ejemplo,
prueba.ps, introduciendo:
$ ps2pdf prueba.ps
obtendrá otro archivo de nombre prueba.pdf en el mismo directorio.
Crear imposiciones
Antes de seguir, debe dirigirse la sección Descargar el manual y archivos asociados y descargar imposiciones.tgz en algún directorio. Descomprímalo, por ejemplo, en Linux, con la orden:
$ tar zxvf imposiciones.tgz
Si utiliza Windows, puede usar winzip o winrar. En cualquier caso, se creará un directorio de nombre imposiciones. Sitúese en él. Este será nuestro lugar de trabajo.
Imposiciones a 2 páginas
Seguramente, éste será el caso que más utilice. Como se ha explicado antes, el archivo origen debe estar en formato postscript (ps). La idea es la siguiente:
Debe agrupar las hojas en cuadernillos, para su posterior encuadernación, y debe decidir cuántas hojas forman el cuadernillo. Un valor razonable es 4 (o 5, tenga en cuenta que después debe coserlo), con lo que cada hoja consta de 4 páginas (2 delanteras y 2 traseras) y el cuadernillo, suma, por tanto, un total de 16 páginas.
Para aclararnos, supongamos que formamos cuadernillos de 4 hojas. Entonces, la disposición correcta es:
|
Hoja primera del primer cuadernillo. |
|

|

|
|
Hoja segunda del primer cuadernillo. |
|
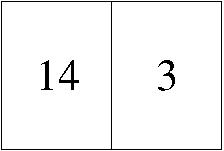
|
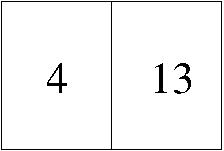
|
|
Hoja tercera del primer cuadernillo. |
|
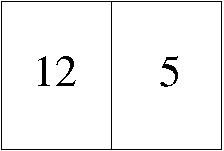
|

|
|
Hoja cuarta del primer cuadernillo. |
|
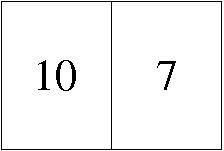
|
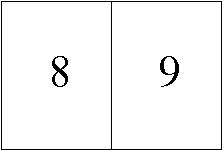
|
Sitúe ahora las hojas de la siguiente forma:
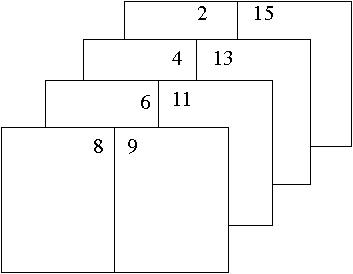
Júntelas. Dóblelas por el segmento vertical central y hacia la derecha de forma que las páginas 8 y 9 queden enfrentadas, y ya tiene el primer cuadernillo. Asegúrese que las páginas están en el orden natural.
Para el segundo cuadernillo, sume 16 a todos los números y listo. Para el tercer cuadernillo, sume 32 y así sucesivamente (16 más que el anterior cada vez que comience un nuevo cuadernillo), aunque no es necesario esta regla, ya que cuando aprenda a hacer bien el primero, los demás le saldrán automáticamente.
Método a seguir
Suponemos que Vd. tiene un documento en formato postscript y quiere hacer una imposición a 2 páginas. Para practicar, utilice 16paginas.ps que se acompaña. Abra un emulador de terminal, por ejemplo xterm, sitúese en el directorio donde está situado el archivo y escriba:
$ psbook -s16 16paginas.ps auxiliar1.ps
la opción -s16 (todo junto, sin espacio de separación entre la s y el 1) es porque nuestro cuadernillo va a tener 16 páginas. Si quiere cuadernillos de n nojas, debe multiplicar por 4, ya que cada hoja consta de 4 páginas. Por ejemplo:
| Cuadernillos de | Opción a introducir |
|---|---|
| 4 hojas | -s16 |
| 5 hojas | -s20 |
| 6 hojas | -s24 |
El programa psbook reordena las hojas del postscript fuente (16paginas.ps) y deja el resultado en auxiliar1.ps. No debe imprimir este último, pues falta un segundo paso. Para ello, introduzca:
$ psnup -2 auxiliar1.ps definitivo.ps
y listo. En el archivo definitivo.ps tiene la imposición a 2 páginas. Si ahora convierte este archivo a pdf, en concreto:
$ ps2pdf definitivo.ps
obtendrá definitivo.pdf.
Imposiciones a 4 páginas
Una imposición a 4 páginas en una hoja A4 es ideal para una agenda de bolsillo. Para comprender bien las operaciones matemáticas que siguen debe leerse el documento dimensionesdin.pdf que resulta al desempaquetar imposiciones.tgz.
En este punto, suponemos que tiene un documento en formato postscript, que llamaremos genéricamente prueba.ps, sobre el cual vamos a hacer todas las manipulaciones, las cuales, en ningún caso alteran su contenido.
Para conseguir las imposición utilizamos el programa pstops (incluído dentro de psutils), el cual dispone de muchas opciones, de las cuales, aquí emplearemos algunas. Este programa tiene como elemento primitivo una página y todo lo demás se construye sobre ella. Conviene distinguir entre página y hoja, en concreto, y debido a las condiciones que hemos supuesto, una hoja será siempre un A4 y una página es cada una de las páginas del documento prueba.ps. En este apartado, una hoja va a contener 8 páginas, 4 en la delantera y 4 en la trasera (ver siguiente figura):

Observe como todas las páginas están reducidas. También, todas, salvo la 8 y la 2 estás desplazadas, y otras, como las 5,4,3,6, están giradas un ángulo de 180°.
Conviene también aprender a diferenciar los conceptos de número físico y número lógico de página. Algunos documentos, comienzan con una introducción en números romanos y el resto con la numeración arábiga habitual 1,2,3,..., a la cual llaman lógica. Si, por ejemplo, dicha introducción tiene 15 páginas (I,II,III,...,XIV,XV) y el resto 200 (1,2,...,200), entonces:
| Número físico de página |
Número lógico de página |
|---|---|
| 1 | 1 |
| 1 | I |
| 2 | II |
| 3 | III |
| ... | ... |
| 15 | XV |
| 16 | 1 |
| 17 | 2 |
| 18 | 3 |
| ... | ... |
| 215 | 200 |
El programa pstops utiliza el concepto de módulo. Para nuestro propósito, módulo es el número de páginas que van a entrar en una hoja. En este apartado de imposición a 4 páginas, el módulo es 8 (4 por la cara delantera y 4 por la trasera). El índice de una página es el siguiente número:
(p-1) mód. 8
siendo p el número físico de la página. Recordamos aquí que a mód. b es el resto de la división entera entre a y b. Por ejemplo, 15 mód. 6 es 3, ya que al dividir 15 entre 6 sale un cociente de 2 y un resto de 3. Análogamente, 8 mód. 4 es 0, pues al dividir 8 entre 4 sale un cociente de 2 y un resto de 0. Entonces:
índice de la página 1 = (1-1) mód. 8 = 0 mód. 8 = 0
índice de la página 2 = (2-1) mód. 8 = 1 mód. 8 = 1
índice de la página 3 = (3-1) mód. 8 = 2 mód. 8 = 2
...
índice de la página 8 = (8-1) mód. 8 = 7 mód. 8 = 7
índice de la página 9 = (9-1) mód. 8 = 8 mód. 8 = 0
índice de la página 10 = (10-1) mód. 8 = 9 mód. 8 = 1
|
Cuadernillo primero |
|
|---|---|
|
Número de página |
Índice pstops |
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| ... | ... |
| 7 | 6 |
| 8 | 7 |
|
Cuadernillo segundo |
|
|---|---|
|
Número de página |
Índice pstops |
| 9 | 0 |
| 10 | 1 |
| 11 | 2 |
| ... | ... |
| 15 | 6 |
| 16 | 7 |
y así sucesivamente. La forma de trabajo de pstops es la siguiente: procesa el primer cuadernillo, donde hemos de decir qué hacer con las páginas, las cuales deben estar especificadas como índices, después el cuadernillo segundo y así sucesivamente hasta acabar el documento.
Operaciones con las páginas
El programa pstops utiliza coordenadas cartesianas, exactamente igual que en la geometría habitual, estando situado el origen de coordenadas O(0,0) en la esquina inferior izquierda de la hoja. Para no tener que andar especificando longitudes numéricas, pstops tiene como variables definidas:
w = ancho de la hoja
h = alto de la hoja
Así pues, la situación inicial para cualquier página A4 es:
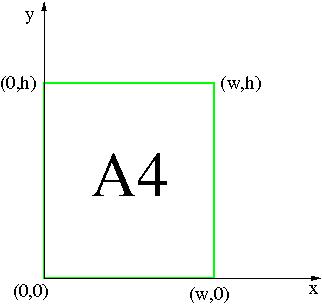
Suponemos que ha leído el documento dimensionesdin.pdf, si no, debe hacerlo ahora, para que las ideas que siguen resulten claras. Comenzamos ya con las operaciones.
Ampliar o reducir una página
Esta operación corresponde al concepto matemático de homotecia, la cual está determinada cuando se da el centro y la razón, que también llamaremos factor de escala. En todos los casos, suponemos que:
- El centro de homotecia es el origen O(0,0).
- Siempre vamos a reducir páginas, por lo cual la razón de homotecia o factor de escala k es menor que la unidad, es decir, k < 1
Una homotecia de razón
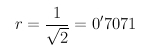
transforma un rectángulo con las dimensiones de un A4 en otro rectángulo con las dimensiones de un A5, lo cual lo expresamos brevemente diciendo que transforma un A4 en un A5, es decir:

Observemos la siguiente figura:

donde en color verde se muestra un A4 y en rojo un A5, m es la mediatriz del segmento OC. Si ahora hacemos lo mismo con un A5 obtenemos un A6, es decir:

Podemos pasar directamente del A4 al A6 multiplicando las razones de homotecia, es decir, como:
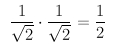
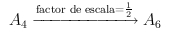
Todas las explicaciones matemáticas de porqué esto es así, se dan en dimensionesdin.pdf, razón por la cual, insisto, su lectura es obligatoria. No obstante, a modo de resumen, tenemos:
-
Para hacer una imposición a 2 páginas, es decir, colocar 2
páginas A5 en la cara delantera de un A4, debe reducir las
páginas según el factor de escala:
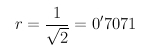
-
Para hacer una imposición a 4 páginas, es decir, colocar 4
páginas A6 en la cara delantera de un A4, debe reducir las
páginas según el factor de escala:
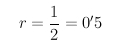
-
Para hacer una imposición a 8 páginas, es decir, colocar 8
páginas A7 en la cara delantera de un A4, debe reducir las
páginas según el factor de escala:
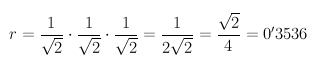
@0.7071 @0.5 @0.3536
Más adelante, describiremos la sintaxis conjunta de todas las
operaciones matemáticas.
Girar una página
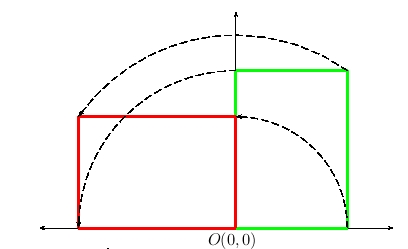
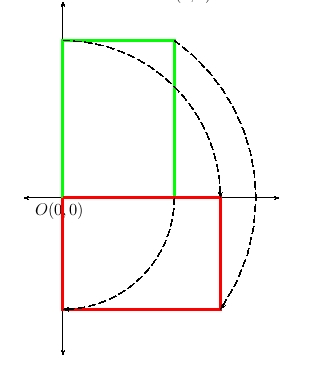
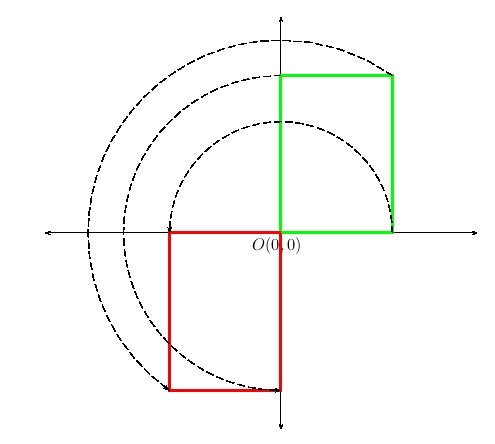
Un giro está completamente determinado cuando se da el centro y el ángulo de giro. El centro en lo que nos ocupa es el origen O(0,0). Solamente disponemos de tres tipos que son:
- Giro de 90° a la izquierda, sintaxis L.
- Giro de 90° a la derecha, sintaxis R.
- Giro de 180°, sintaxis U. En este caso da igual si es a derecha o izquierda, ya que el resultado final es el mismo. Debe resultar evidente que un giro de 180° es igual que una simetría respecto del origen de coordenadas.
Desplazar una página
Puede trasladar una página según un vector v = (a,b). El significado es el mismo que en matemáticas. Observe la siguiente figura:
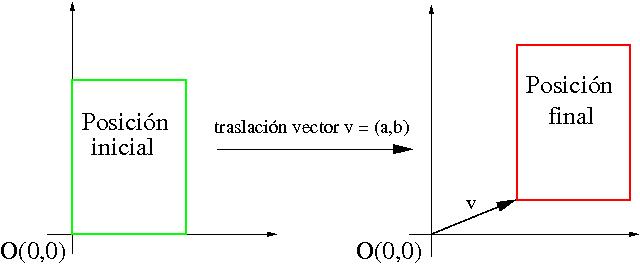
Si no tiene conocimientos matemáticos, la siguiente interpretación le ayudará a entenderlo.
| Coordenada a | Significado |
| positiva | desplazamiento a la derecha |
| negativa | desplazamiento a la izquierda |
| nula | sin movimiento a izquierda y derecha |
| Coordenada b | Significado |
| positiva | desplazamiento hacia arriba |
| negativa | desplazamiento hacia abajo |
| nula | sin movimiento arriba ni abajo |
- v = (1,2), quiere decir desplazar la figura 1 m. a la derecha y después 2 m. hacia arriba.
- v = (0,-2), quiere decir desplazar la figura 2 m. hacia abajo.
- v = (-1,0), quiere decir desplazar la figura 1 m. a la izquierda.
- v = (2,-1), quiere decir desplazar la figura 2 m. a la derecha y 1 m. hacia abajo.
Sintaxis pstops para las Operaciones con las páginas
Es la siguiente:
i[L][R][U][@factorescala][(a,b)]
siendo i el índice de la página y los corchetes alrededor
de una operación significa que es opcional, pero que, en caso de
utilizarla, no se deben incluir. Para entenderlo, volvamos a la
figura:

La página 8, cuyo índice es 7, debe reducirse en un factor de 0.5, sin embargo, no debe desplazarse ni girarse, por tanto, las operaciones para ella serían:
7@0.5
La página 1, cuyo índice es 0, debe reducirse también según el factor de 0.5, no debe girarse, pero sí desplazarse a la derecha según el vector (0.5w,0) (ver figura):
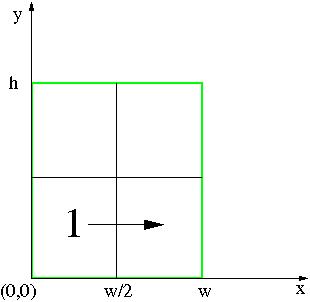
luego, las operaciones para ella serían:
0@0.5(0.5w,0)
La página 5, cuyo índice es 4, debe reducirse también según el factor de 0.5, girarse 180° y desplazarse una distancia w/2 a la derecha y 1h hacia arriba (ver figura):
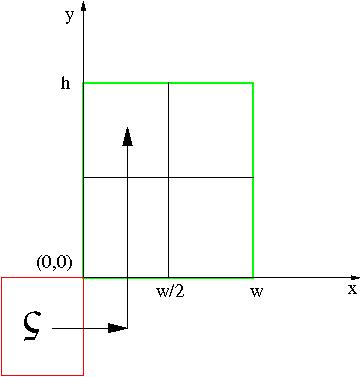
luego, las operaciones para ella serían:
4U@0.5(0.5w,1h)
Por último para la página 4, cuyo índice es 3 (ver figura):
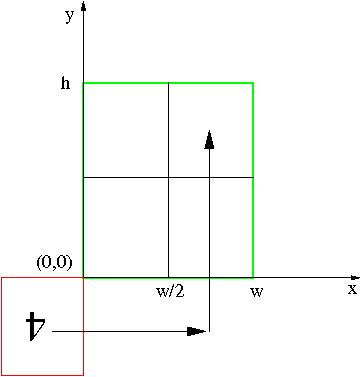
luego, las operaciones para ella serían:
3U@0.5(1w,1h)
Ahora tenemos que juntarlas todas, lo cual se hace con el operador suma +, que actúa como separador de páginas dentro de una hoja. Por consiguiente, recopilando resultados:
7@0.5+0@0.5(0.5w,0)+4U@0.5(0.5w,1h)+3U@0.5(1w,1h)
Queda ahora por hacer la parte trasera, que es idéntica a esta, salvo cambiando los índices, y hay que saber que para separar la delantera de la trasera, utilizamos el operador coma ,. Por último, el módulo, 8 en este caso, se coloca al comienzo y se separa de todo el resto con el operador :, así que finalmente, todas las operaciones quedan como:
8:7@0.5+0@0.5(0.5w,0)+4U@0.5(0.5w,1h)+3U@0.5(1w,1h),
1@0.5+6@0.5(0.5w,0)+2U@0.5(0.5w,1h)+5U@0.5(1w,1h)
y programa pstops completo. Se han separado en dos filas
para facilitar la lectura, aunque todo debe escribirse en una
única línea.
Asalto final
En mi sistema linux, el papel por defecto que usa pstops es A4, pero, en otras distribuciones es letter, razón por la cual, no podemos permitirnos asumir que los valores por defecto son los correctos para lo que pretendemos hacer. Una opción de pstops es indicar el tamaño del papel en línea de órdenes mediante la opción -p seguida del tamaño, en nuestro caso, a4. En conclusión, volviendo a nuestro convenio inicial de que queríamos hacer las imposiciones a 4 páginas sobre prueba.ps, el programa quedaría así (todo en una línea, lo ponemos en dos para facilitar la lectura):
pstops -pa4 '8:7@0.5+0@0.5(0.5w,0)+4U@0.5(0.5w,1h)+3U@0.5(1w,1h),
1@0.5+6@0.5(0.5w,0)+2U@0.5(0.5w,1h)+5U@0.5(1w,1h)' prueba.ps resultado.ps
Veamos unos comentarios finales:
- Son necesarios los apóstrofos (') para evitar la interpretación por parte del shell de los metacaracteres.
-
En resultado.ps está la imposición a 4 páginas hecha
tomando como fuente prueba.ps, el cual no queda
alterado. Puede omitir este argumento y el resultado saldrá
por la pantalla. En concreto:
pstops -pa4 '8:7@0.5+0@0.5(0.5w,0)+4U@0.5(0.5w,1h)+3U@0.5(1w,1h), 1@0.5+6@0.5(0.5w,0)+2U@0.5(0.5w,1h)+5U@0.5(1w,1h)' prueba.ps
Puede utilizar los operadores de redirección del shell, por ejemplo:$ pstops -pa4 '8:7@0.5+0@0.5(0.5w,0)+4U@0.5(0.5w,1h)+3U@0.5(1w,1h), 1@0.5+6@0.5(0.5w,0)+2U@0.5(0.5w,1h)+5U@0.5(1w,1h)' prueba.ps > resultado.psy obtendrá lo mismo que al principio. -
Observe que hemos conseguido manipular archivos
postscript sin conocer éste lenguaje, lo cual hace que
éste tipo de utilidades sean realmente grandes. Por otro lado,
si tiene alguna pega, pruebe con las ayudas del sistema, que a
veces aclaran las ideas:
$ man pstops
o también$ info pstops
Archivos contenidos en imposiciones.tgz
- 8paginas.ps y 16paginas.ps. Archivos postscript para hacer prácticas. El primero (resp. el segundo) contiene 8 (resp. 16) páginas cuyo contenido es el número de página en tamaño grande.
- agenda.ps y agenda.tex. Simulación aleatoria de una hipotética agenda.
- dimensionesdin.pdf. Documento donde se explican ciertas cuestiones matemáticas necesarias para entender las operaciones del programa pstops.
- modelo4.ps, modelo4.pdf, modelo8.ps, modelo8.pdf. Archivos auxiliares comentados antes.
- impo4, impo8. Programas shell para hacer las imposiciones. El uso de ellos se comenta a continuación.
Programa impo4
Contiene las instrucciones ya comentadas anteriormente para hacer una imposición a 4 páginas. Veamos cómo utilizarlo.- Descargue imposiciones.tgz. Suponemos que lo ha hecho en el subdirectorio maniobras de su directorio de inicio.
-
Abra un emulador de terminal, por ejemplo, xterm y
sitúese en maniobras. Desempaquete:
pedro@servidor:~/maniobras> tar zxvf imposiciones.tgz imposiciones/ imposiciones/agenda.tex imposiciones/agenda.ps imposiciones/impo4 imposiciones/impo8 imposiciones/modelo4.pdf imposiciones/modelo8.pdf imposiciones/dimensionesdin.pdf imposiciones/16paginas.ps imposiciones/modelo4.ps imposiciones/modelo8.ps imposiciones/8paginas.ps
La orden anterior crea un subdirectorio de nombre imposiciones. Sitúese en él:cd imposiciones
Haga un listado:pedro@servidor:~/maniobras/imposiciones> ls -al total 480 drwxr-xr-x 2 pedro users 392 2009-03-14 11:59 ./ drwxr-xr-x 3 pedro users 112 2009-03-14 12:04 ../ -rw-r--r-- 1 pedro users 3138 2009-03-14 11:59 16paginas.ps -rw-r--r-- 1 pedro users 1619 2009-03-14 11:59 8paginas.ps -rw-r--r-- 1 pedro users 203060 2009-03-14 11:59 agenda.ps -rw-r--r-- 1 pedro users 172388 2009-03-14 11:59 agenda.tex -rw-r--r-- 1 pedro users 65096 2009-03-14 11:59 dimensionesdin.pdf -rwxr-xr-x 1 pedro users 132 2009-03-14 11:59 impo4* -rwxr-xr-x 1 pedro users 317 2009-03-14 11:59 impo8* -rw-r--r-- 1 pedro users 1652 2009-03-14 11:59 modelo4.pdf -rw-r--r-- 1 pedro users 5915 2009-03-14 11:59 modelo4.ps -rw-r--r-- 1 pedro users 1959 2009-03-14 11:59 modelo8.pdf -rw-r--r-- 1 pedro users 10349 2009-03-14 11:59 modelo8.ps
-
Observe que impo4 e impo8 tienen los
permisos de ejecución. Por si acaso, asegúrese:
pedro@servidor:~/maniobras/imposiciones> chmod +rx impo4 impo8
-
Ahora hacemos una imposición a 4 páginas con
16paginas.ps, dejando el resultado en
resultado1.ps:
pedro@servidor:~/maniobras/imposiciones> ./impo4 16paginas.ps resultado1.ps [1] [2] [3] [4] Wrote 4 pages, 10089 bytes
y lo vemos:pedro@servidor:~/maniobras/imposiciones> gv resultado1.ps
-
Ahora hacemos una imposición a 8 páginas con
16paginas.ps, dejando el resultado en
resultado1.ps:
pedro@servidor:~/maniobras/imposiciones> ./impo8 16paginas.ps resultado1.ps [1] [2] Wrote 2 pages, 10349 bytes
y lo vemos:pedro@servidor:~/maniobras/imposiciones> gv resultado1.ps
Archivos TeX
Veamos todos los pasos para conseguir la agenda, partiendo del fuente. las condiciones, igual que antes, es decir, ha abierto un emulador de terminal y está situado en imposiciones.- Procese el fuente:
pedro@servidor:~/maniobras/imposiciones> latex agenda This is pdfeTeX, Version 3.141592-1.21a-2.2 (Web2C 7.5.4) entering extended mode ....Mucha información va aquí (se omite)
La orden anterior crea el .dvi. Comprobamos:pedro@servidor:~/maniobras/imposiciones> ls -l total 616 -rw-r--r-- 1 pedro users 3138 2009-03-14 11:59 16paginas.ps -rw-r--r-- 1 pedro users 1619 2009-03-14 11:59 8paginas.ps -rw-r--r-- 1 pedro users 265 2009-03-14 12:14 agenda.aux -rw-r--r-- 1 pedro users 111360 2009-03-14 12:14 agenda.dvi -rw-r--r-- 1 pedro users 7683 2009-03-14 12:14 agenda.log -rw-r--r-- 1 pedro users 203060 2009-03-14 11:59 agenda.ps -rw-r--r-- 1 pedro users 172388 2009-03-14 11:59 agenda.tex -rw-r--r-- 1 pedro users 65096 2009-03-14 11:59 dimensionesdin.pdf -rwxr-xr-x 1 pedro users 132 2009-03-14 11:59 impo4 -rwxr-xr-x 1 pedro users 317 2009-03-14 11:59 impo8 -rw-r--r-- 1 pedro users 1652 2009-03-14 11:59 modelo4.pdf -rw-r--r-- 1 pedro users 5915 2009-03-14 11:59 modelo4.ps -rw-r--r-- 1 pedro users 1959 2009-03-14 11:59 modelo8.pdf -rw-r--r-- 1 pedro users 10349 2009-03-14 11:59 modelo8.ps -rw-r--r-- 1 pedro users 10349 2009-03-14 12:09 resultado1.ps
-
Cree el postscript. Para no destruir la agenda original
agenda.ps, escribimos:
pedro@servidor:~/maniobras/imposiciones> dvips -o agenda2.ps agenda.dvi This is dvips(k) 5.95a Copyright 2005 Radical Eye Software (www.radicaleye.com) ' TeX output 2009.03.14:1214' -> agenda2.ps <tex.pro><texps.pro>. <cmsl12.pfb><cmr12.pfb><cmsy10.pfb><cmbx12.pfb> <cmr17.pfb>[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78]
-
Observe que agenda2.ps tiene 78 páginas. Si desea
utilizar, por practicar, solo una parte, use el programa psselect,
contenido también en psutils. Por ejemplo, para
seleccionar las 16 primeras, escriba:
pedro@servidor:~/maniobras/imposiciones> psselect -p1-16 agenda2.ps otragenda.ps [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] Wrote 16 pages, 92786 bytes
Y en otragenda.ps tiene solo las 16 primeras páginas de la agenda. -
Hacemos ahora las imposiciones a 4 y a 8 páginas:
pedro@servidor:~/maniobras/imposiciones> ./impo4 agenda2.ps resultado1.ps [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] Wrote 20 pages, 231318 bytes pedro@servidor:~/maniobras/imposiciones> ./impo8 agenda2.ps resultado2.ps [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Wrote 10 pages, 232608 bytes
y los vemos:pedro@servidor:~/maniobras/imposiciones> gv resultado1.ps pedro@servidor:~/maniobras/imposiciones> gv resultado2.ps
Imposiciones a 8 páginas
Sin más explicaciones, mostramos aquí la colocación de las páginas:

|

|
pstops -pa4 '16:0R@0.354(0,0.25h)+15R@0.354(0,0.5h)+12R@0.354(0,0.75h)+
3R@0.354(0,1h)+7L@0.354(1w,0)+8L@0.354(1w,0.25h)+11L@0.354(1w,0.5h)+
4L@0.354(1w,0.75h),6R@0.354(0,0.25h)+9R@0.354(0,0.5h)+10R@0.354(0,0.75h)+
5R@0.354(0,1h)+1L@0.354(1w,0)+14L@0.354(1w,0.25h)+13L@0.354(1w,0.5h)+
2L@0.354(1w,0.75h)' $1 $2
Notas finales
- Todo este artículo se ha hecho en el sistema operativo Linux.
- Los documentos tex, Makefiles, programas, html, hojas de estilos, etc. se editaron con Emacs.
- Para la simulación aleatoria de las personas en la agenda (agenda.tex) se utilizó Mysql y PHP.
- Algunas imágenes están hechas con xfig y exportadas a jpg. Otras con Pstricks y mediante ImageMagick capturadas a jpg.
- Los programas para crear las imposiciones pstops, psbook, psnup, psselect, etc., pertenecen al paquete psutils.